Author Archives: nxnhat

LỜI GIẢI BÀI HÌNH ĐỀ THI IMO 2017 NGÀY 2

By

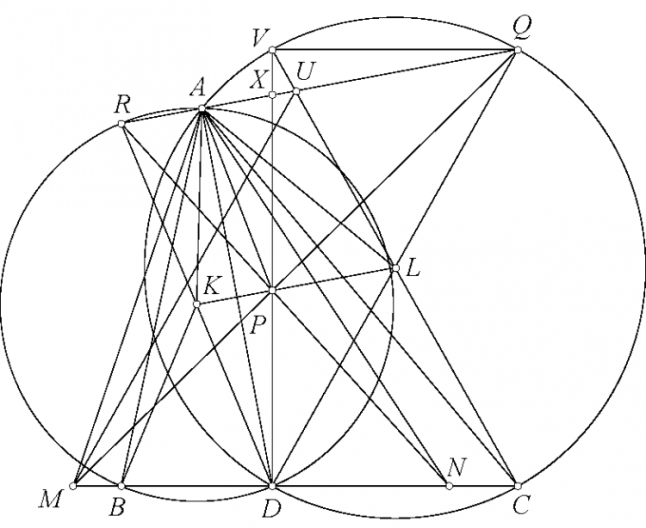
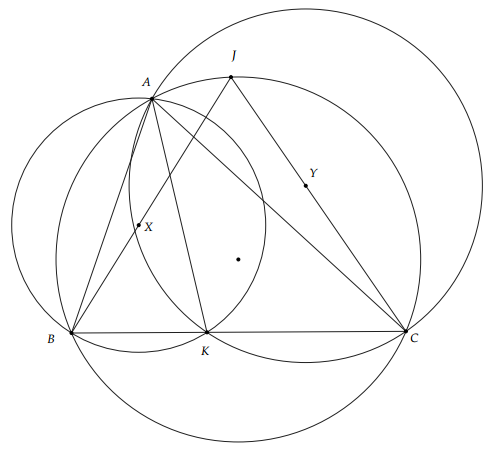
Đề bài: Cho R và S là hai điểm phân biệt trên đường tròn \Omega sao cho RS không phải là đường kính. Cho \ell là tiếp tuyến tại R của \Omega. Lấy điểm T sao cho S là trung điểm của đoạn thẳng RT. Lấy điểm J trên cung nhỏ RS của \Omega sao cho đường tròn ngoại tiếp \Gamma của tam giác JST cắt \ell tại hai điểm phân biệt. Gọi A  là giao điểm gần R nhất của \Gamma và \ell. Đường thẳng AJ cắt lại \Omega tại K. Chứng minh rằng KT tiếp xúc với \Gamma.

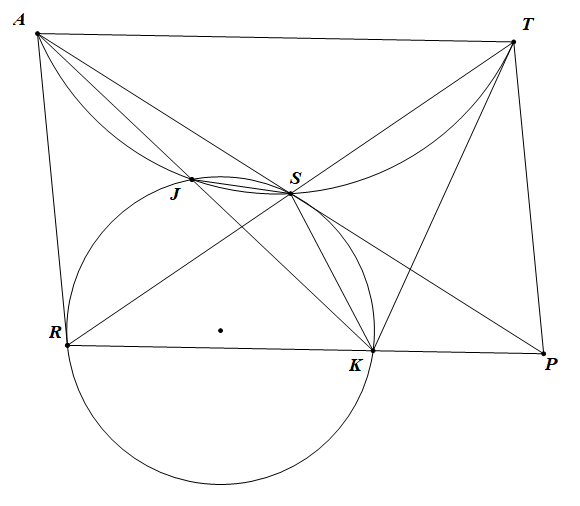
imo ngay 2 2017

Ta có:

\angle ATS = \angle SJK = \angle KRS \Rightarrow  AT \parallel RK  

Ta thấy S là trung điểm RT nên từ đây ta lấy P đối xứng với A qua S. Từ đây suy ra ATPR là hình bình hành

\angle RPT = \angle RAT = \angle RSK   Suy ra S, K, P, T đồng viên.
Suy ra: \angle STK = \angle SPK = \angle SAT nên KT là tiếp tuyến của \Gamma nên KT tiếp xúc với \Gamma. \square

Đề thi IMO năm nay cả hai ngày chỉ có một bài hình phẳng và nó không khó lắm. Thật ra ý tưởng của bài này là dựng ra hình bình hành không quá xa lạ lắm. Nó xuất hiện rất phổ biến và đặc biệt từ các đề thi các cấp của lớp 9 nên bài này ngay cả học sinh THCS cũng có thể giải được. Sau đây là một số bài toán sau tương tự về mặt ý tưởng:

Bài 1:   (Nguyễn Minh Hà) Cho tam giác ABC có trực tâm H. Gọi M,N lần lượt là trung điểm của AH,BC. Gọi P,Q lần lượt là chân đường vuông góc hạ từ N xuống BH,CH.Chứng minh rằng MN đi qua trung điểm của PQ.

Bài 2: Cho \triangle ABC nội tiếp (O), trực tâm H, M là trung điểm của BC. AM cắt (O) tại P. Gọi X là điểm đối xứng của P qua M. Trên (O) lấy Q sao cho AQ là đường đối trung của \triangle ABC. Chứng minh X là hình chiếu của H lên AM và X là điểm đối xứng của Q qua BC.

Bài 3:  Cho tam giác ABC nhọn nội tiếp đường tròn (O) có trực tâm là H. D là điểm trên cung nhỏ BC. Lấy E sao cho ADCE là hình bình hành và K là trực tâm tam giác ACE. Gọi P, Q lần lượt là hình chiếu của K trên BC và AB. Chứng minh rằng: PQ đi qua trung điểm HK.

Lời giải một bài toán hình học THCS hay

By

Đề bài: (Thầy Trần Quang Hùng – HSGS đăng trong Topic ôn thi hình vào cấp 3 – VMF)

Cho tam giác ABC có D nằm trên đoạn BC. (K),(L) lần lượt là đường tròn ngoại tiếp các tam giác ADB,ADC. DR,DQ là đường kính của (K),(L). P thuộc đoạn KL sao cho DP\perp BC. QP,RP lần lượt cắt BC tại M,N. Chứng minh rằng \angle MAN=\angle BAC.

post-118251-0-99640100-1492690212

Lời giải:
Gọi CV là đường kính của (L). U thuộc CV sao cho MU\parallel DL. Gọi DP cắt QR tại X thì P là trung điểm DX. Ta có \frac{VL}{UL}=\frac{CL}{UL}=\frac{CD}{MD}=\frac{QV}{MD}=\frac{PV}{PD}=\frac{VP}{PX} do đó XU\parallel PL\parallel QR nên U thuộc QR. Từ đó \angle AUM = \angle AQD=\angle ACD do đó tứ giác AUCM nội tiếp. Dễ thấy tam giác UMC cân do tam giác LDC cân nên AX là phân giác ngoài \angle MAC. Tương tự AX cũng là phân giác ngoài \angle NAB nên \angle MAN=\angle BAC.

Nhận xét: Đây là một bài toán khá lạ và rất hay đối với học sinh THCS. Ngoài ra ta có thể sử dụng hàng điểm điều hòa nhưng ở đây phạm vi kiến thức là THCS nên việc dùng như thế không hợp lí.
Tham khảo thêm cách sử dụng hàng điểm: Lời giải khác

Tôi sẽ cố gắng đăng thêm nhiều bài toán hay như thế.

 

 

Lời giải bài hình đề thi tuyển sinh vào lớp 10 vòng 1 Hà Nội 2017-2018

By
Đề bài: Cho đường tròn (O) ngoại tiếp tam giác ABC. Gọi M,N lần lượt là điểm chính giữa cung nhỏ AB và cung nhỏ BC. AN \cap CM = I. Dây MN cắt cạnh AB và BC lần lượt tại H,K.
a) Chứng minh: C,N,K,I đồng viên.
b) Chứng minh: NB^{2} = NK.NM.
c) Chứng minh : BHIK là hình thoi.
d) Gọi P,Q lần lượt là tâm các đường tròn ngoại tiếp tam giác MBK, MCK. Gọi E là trung điểm PQ.Vẽ đường kính ND của đường tròn (O). Chứng minh: D,E,K thẳng hàng.
vong1ams
a) Do \angle KNI = \angle ACM =\angle ICK \Rightarrow C,I,K,N đồng viên.
b) Vì \angle NBK = \angle NCK = \angle BMN \Rightarrow \bigtriangleup BKN \sim \bigtriangleup MBN \Rightarrow NB^{2} = MN. NK
c) Ta có: KICN nội tiếp do đó \angle HKI = \angle MCN = \angle KHB. Do đó BH // KI . Tương tự thì HI // BK . Chú ý KH là phân giác \angle BKI nên HIKB là hình thoi.

d) Bổ đề:Cho tam giác ABC nội tiếp đường tròn (O) có K thuộc BC. Gọi X,Y lần lượt là tâm (ABK), (AKC). Chứng minh rằng BX và CY cắt nhau trên (O).

bode

Chứng minh: Ta chứng minh trong trường hợp hình vẽ này, các trường hợp khác chứng minh tương tự . Gọi CY \cap (O) = J \neq C. Ta có:
\angle JBA = \angle JCA = 90^{\circ} - \dfrac{\angle AY C }{2} = \dfrac{180^{\circ}-(360^{\circ}-2 \angle AKC )}{2}=\angle AKC - 90^{\circ} = 90^{\circ} \angle AKB = \angle XBA
Do đó B,X,J thẳng hàng.

Quay lại bài toán. Ta quy bài toán về chứng minh DPKQ là hình bình hành. Áp dụng bổ đề trên thì BP cắt CQ tại D' trên (O).

Mà :
\angle D'BC = 90^{\circ} - \dfrac{ \angle BPK }{2} = 90^{\circ} - \angle KMB =90^{\circ} -\angle KMC = \angle DCB
Do đó D \equiv D'. Thế nên \angle DPK = \angle DQK . Vậy mà:
\angle PKQ = 180^{\circ} - \angle PKB - \angle QKC = 180^{\circ} - 2(90^{\circ} -\angle KMC ) = \angle BMC = \angle BDC
Do đó DPKQ là hình bình hành nên DK đi qua trung điểm E của PQ.